导数:相关变化率与滑梯问题
关于相关变化率
如果已知其中一个变化率,由一个关系式可求出与之相关的另一个变化率,这就是所谓的相关变化率(related rates)问题。解决相关变化率的问题,首先要建立这两个相关变量的一个等式,然后对时间求导(如果这两个变量都对时间可导),找到相关变化率的关系。通过数学语言可将相关变化率描述为: 变量$x$和$y$是由一个方程$F(x,y)=0$联系着,$x$和$y$都是时间$t$的可导函数:$x=x(t), y=y(t)$。利用链式法则将方程$F[x(t), y(t)]=0$关于时间$t$求导,可得变化率$\frac{dx}{dt}$和$\frac{dy}{dt}$之间的一个等式。在建立这个等式之前等式,先了解一下复合函数的求导法则. # 复合函数的求导 设函数$u=g(x)$在点$x$处可导,而函数$y=f(u)$在点$u=g(x)$可导,则复合函数$y=f(u)=f[g(x)]$在点$x$处可导,且有导数: $$ \frac{dy}{dx} = f'(u)g'(x), \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} $$ 这就是复合函数求导的链式法则(The Chain Rule)。复合函数的求导法则可以推广到多个函数的情形,设有可导函数:$y=f(u), u=g(v), v=h(x) \implies y=f(g(h(x)))=y(x)$,则有链式法则: $$ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dv} \cdot \frac{dv}{dx} = f'(u) \cdot g'(v) \cdot v'(x) $$ # 滑梯问题 一个长度为10米的梯子斜靠在垂直的墙壁上。若梯子下端以3米/秒的速度离开墙壁,问当梯子下端距离墙壁6米时,梯子上端向下滑动的速度是多少? 解:设梯子下端距离墙壁$x$米,上端距离地面$h$米,$x$和$h$均为时间的函数。已知下端滑动的速度$dx/dt=3$(米/秒),欲求$x=6$(米)时的$dh/dt$的值(上端向下滑动的速度),先建立$x$和$h$的关系式,根据勾股定理: $$x^2+h^2=10^2$$ 等式两边对时间$t$求导: $$ (x^2+h^2)'_t = (100)'_t $$ 注意对$t$求导时,因为$x$和$h$都是时间$t$的函数,所以应该看成是复合函数的求导,所以: $$ 2x \frac{dx}{dt} + 2h \frac{dh}{dt}= 0 $$ 化简后: $$ \frac{dh}{dt} = −\frac{x}{h} \cdot \frac{dx}{dt} $$ 将$ \frac{dx}{dt}=3,x=6, h=8$代入得到: $$ \frac{dh}{dt} = −\frac{6}{8} \cdot 3 = −\frac{9}{4}(米/秒) $$ 此时,梯子上端正以$(\frac{9}{4})米/秒$的速度下滑。(取负值表明$h$随时间$t$的增加而减少)。
QkCalc中的求导和滑梯问题演示
在QkCalc中,在计算模式下,通过开始菜单中的"导数"插入求导表达式

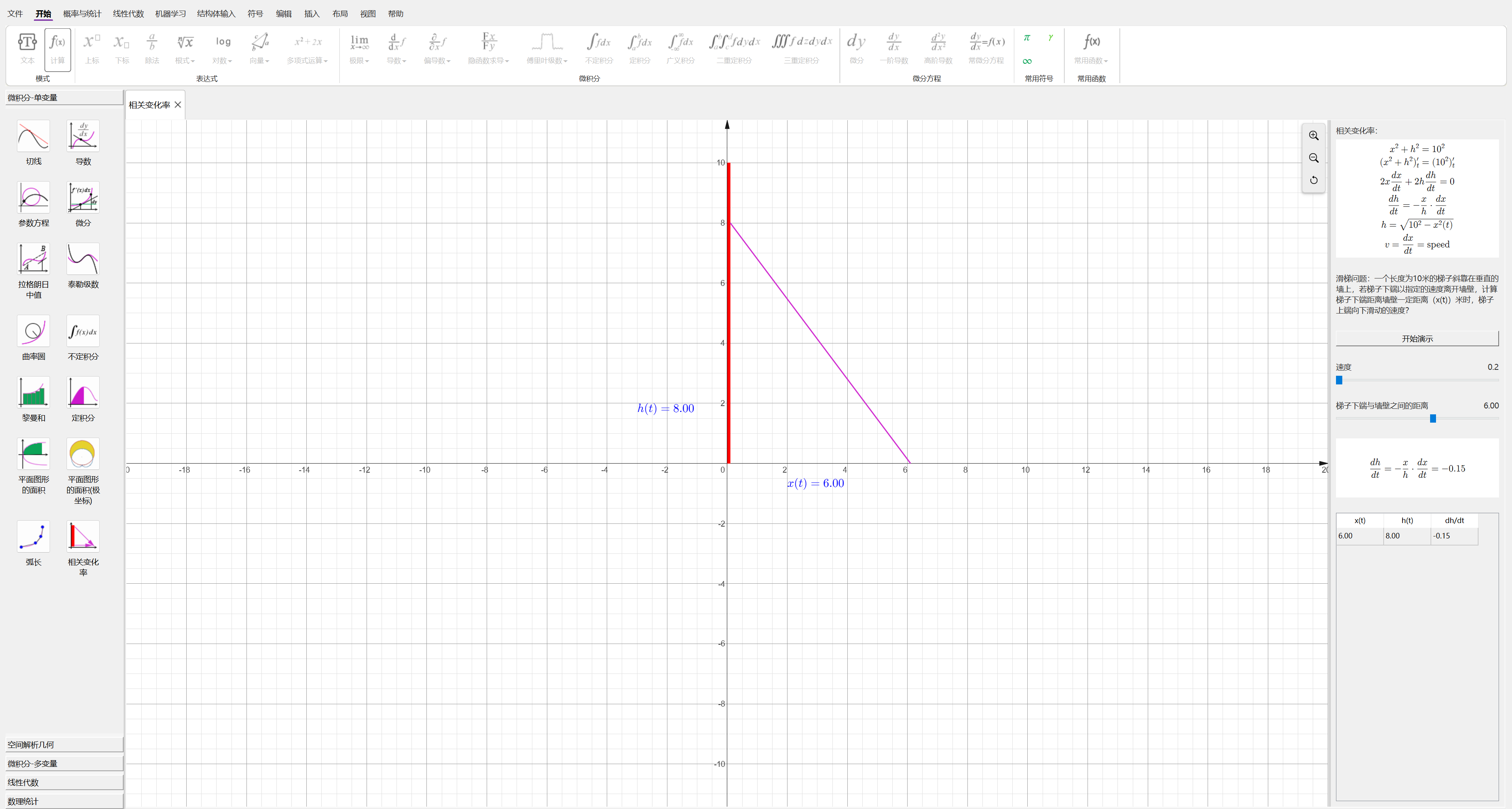
它支持一阶导数和高阶导数,能自动求解复合函数的导数。在解决上述问题时,我们必须将抽象函数的求导具体化。此外,在"微积分-单变量"中的"相关变化率"中,动态演示了如何调整不同速度和距离下的梯子滑动情况。